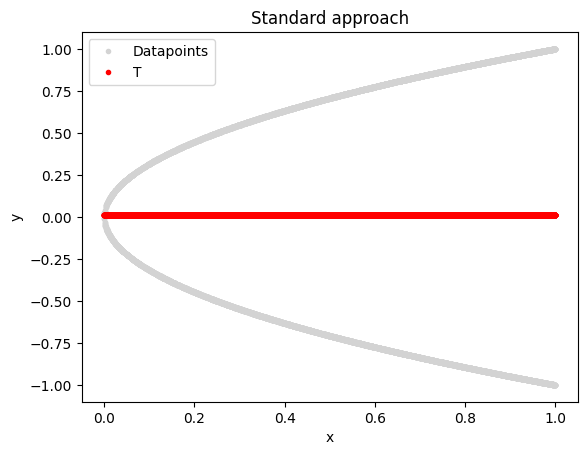
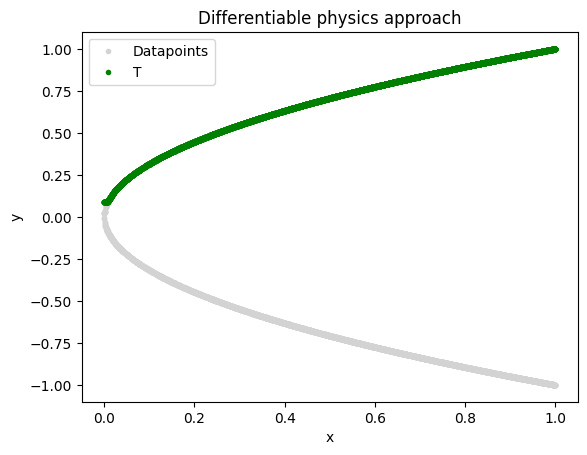
A Probabilistic Generative AI Approach#
As hinted at above, we can do even better with state of the art AI techniques: we can learn the full distribution of the posterior, in our case the different answers for each \(x\). Below, we’ll use flow matching as a state of the art approach from generative, diffusion-based algorithms.
As these methods work with noisy data, we first need to specify a new dataloader, that adds different amounts of “noise” onto the y values of our data, so that the network can learn the right direction towards the two possible modes.
from torch.utils.data import Dataset, DataLoader
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
class FlowMatchingDataset(Dataset):
def __init__(self, data_x, data_y, n_samples=1000, sigma_min=1e-4):
super().__init__()
self.n_samples = n_samples
self.sigma_min = sigma_min
self.data_x = data_x
self.data_y = data_y
def __len__(self):
return self.n_samples
def __getitem__(self, idx):
x0 = np.random.multivariate_normal([0.0, 0.0], np.eye(2), 1)[0]
t = np.random.rand() # scalar in [0,1]
dx = self.data_x[idx] #:idx+1]
dy_org = self.data_y[idx]# :idx+1]
x0[0] = dx[0] # keep x value
x1 = np.concatenate([dx,dy_org],axis=0)
#print([self.data_x.shape,dx.shape,x1.shape])
x_t = (1 - ( 1 - self.sigma_min) * t) * x0 + t * x1
u_t = (x1 - x0)
x_t = torch.tensor(x_t, dtype=torch.float32)
t = torch.tensor([t], dtype=torch.float32)
u_t = torch.tensor(u_t, dtype=torch.float32)
return x_t, t, u_t
The network itself is not much different from before, we only need to add an additional time input t:
class VelocityNet(nn.Module):
def __init__(self, hidden_dim, in_dim=2, time_dim=1, out_dim=2):
super().__init__()
self.net = nn.Sequential(
nn.Linear(in_dim + time_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, out_dim)
)
def forward(self, x, t):
xt = torch.cat([x, t], dim=1)
return self.net(xt)
Training proceeds in line with before, we simply sample noisy samples from the dataset, and train the network to move samples towards the solutions in the dataset:
batch_size = 128
dataset = FlowMatchingDataset(X, Y, n_samples=N)
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
nn_fm = VelocityNet(hidden_dim=128).to(device)
optimizer = optim.Adam(nn_fm.parameters(), lr=0.001)
criterion = nn.MSELoss()
for epoch in range(epochs):
running_loss = 0.0
for x_t, t, u_t in dataloader:
x_t = x_t.to(device)
t = t.to(device)
u_t = u_t.to(device)
optimizer.zero_grad()
pred_v = nn_fm(x_t, t)
loss = criterion(pred_v, u_t)
loss.backward()
optimizer.step()
running_loss += loss.item() * x_t.size(0)
running_loss /= len(dataset)
if(epoch%10==9): print(f"Epoch {epoch + 1}/{epochs}, Loss: {running_loss:.4f}")
Epoch 10/50, Loss: 0.3837
Epoch 20/50, Loss: 0.3773
Epoch 30/50, Loss: 0.3735
Epoch 40/50, Loss: 0.3726
Epoch 50/50, Loss: 0.3715
For evaluation, we now repeatedly call the neural network to improve an initial noisy sample drawn from a simple distribution, and step by step move it towards a “correct” solution. This is done in the integrate_flow function below.
def integrate_flow(nn, x0, t_span=(0.0, 1.0), n_steps=100):
trajectory = []
t = torch.linspace(t_span[0], t_span[1], n_steps).to(x0.device)
dt = 1./n_steps
x_in = x0
for i in range(n_steps):
x0 = x0 + dt * nn(x0, torch.tensor([i/n_steps]).expand(x0.shape[0], 1).to(x0.device) )
x0[:,0] = x_in[:,0] # condition on original x position
trajectory.append(x0)
return trajectory, t
# Generate samples along x, then randomize along y
n_gen = 500
x_in = torch.linspace(0.,1., n_gen).to(device)
y_in = torch.randn(n_gen).to(device) * 0.95
x0_gen = torch.stack([x_in,y_in],axis=-1)
trajectory, time_points = integrate_flow(nn_fm, x0_gen)
To illustrate this flow process, the next cell shows samples at different times in the flow integration. The initial random distribution slowlyl transforms into the bi-modal one for our parabola targets.
import seaborn as sns
sns.set_theme(style="ticks", palette="pastel")
def get_angle_colors(positions):
angles = np.arctan2(positions[:, 1], positions[:, 0])
angles_deg = (np.degrees(angles) + 360) % 360
colors = np.zeros((len(positions), 3))
for i, angle in enumerate(angles_deg):
segment = int(angle / 120)
local_angle = angle - segment * 120
if segment == 0: # 0 degrees to 120 degrees (R->G)
colors[i] = [1 - local_angle/120, local_angle/120, 0]
elif segment == 1: # 120 degrees to 240 degrees (G->B)
colors[i] = [0, 1 - local_angle/120, local_angle/120]
else: # 240 degrees to 360° (B->R)
colors[i] = [local_angle/120, 0, 1 - local_angle/120]
return colors
desired_times = [0.2, 0.6, 0.8,]
time_np = time_points.detach().cpu().numpy()
n_steps = len(time_np)
indices = [np.argmin(np.abs(time_np - t_val)) for t_val in desired_times]
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
axes = axes.ravel() # flatten the 2D array for easier indexing
xx, yy = np.mgrid[0:1:100j, -1:1:100j]
positions = np.vstack([xx.ravel(), yy.ravel()])
for i, idx in enumerate(indices):
ax = axes[i]
x_t = trajectory[idx].detach().cpu().numpy()
if i == 0:
c = get_angle_colors(x_t)
ax.scatter(x_t[:, 0], x_t[:, 1], alpha=0.5, s=10, color=c)
ax.set_title(f"t = {time_np[idx]:.2f}")
ax.grid(True)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
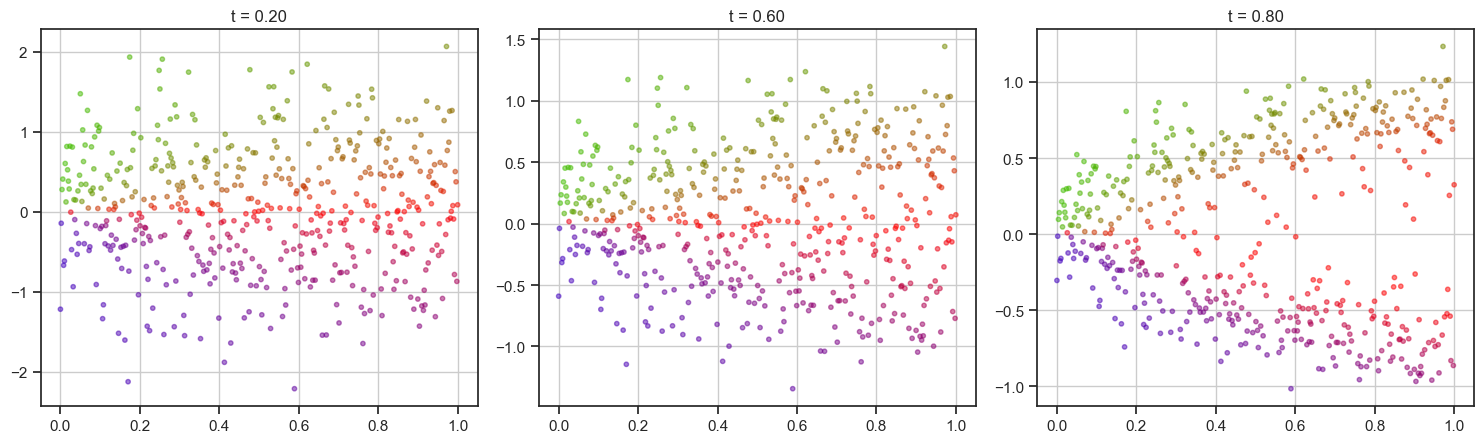
Let’s also plot the solution in line with the supervised and differentiable physics variants above:
# Results
plt.plot(X,Y,'.',label='Datapoints', color="lightgray")
plt.plot(trajectory[-1][:,0].detach().cpu(), trajectory[-1][:,1].detach().cpu(), '.',label='Flow Matching', color="orange")
plt.xlabel('x')
plt.ylabel('y')
plt.title('Probabilistic Version')
plt.legend()
plt.show()
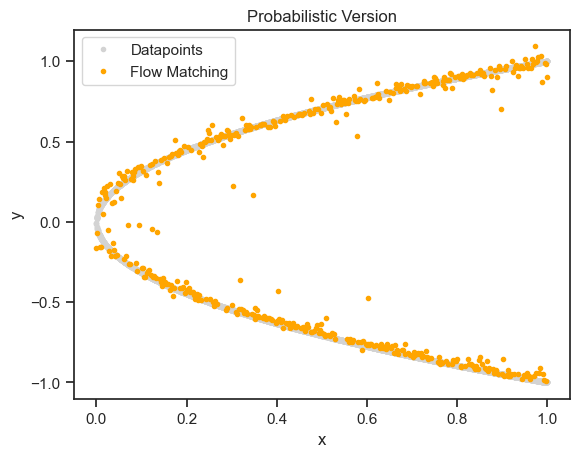
As promised, this approach actually resolves both “modes” of the solution in the form of points above and below the x-axis. It’s still a bit noisy, but this could be alleviated by improving the learning setup, e.g., a larger network would help.
An obvious question here also is: we’re back to training only with data, how about integrating the physics? That’s an obvious point for improvements, and we’ll address diffusion-based methods with physical constraints in more detail in a later section. As an outlook: physics-priors can help especially to drive the somewhat noisy output of a neural network towards an accurate solution.

Discussion#
It’s a very simple example, but it very clearly shows a failure case for supervised learning. While it might seem very artificial at first sight, many practical PDEs exhibit a variety of these modes, and it’s often not clear where (and how many) exist in the solution manifold we’re interested in. Using supervised learning is very dangerous in such cases. We might unknowingly get an average of these different modes.
Good and obvious examples are bifurcations in fluid flow. Smoke rising above a candle will start out straight, and then, due to tiny perturbations in its motion, start oscillating in a random direction. The images below illustrate this case via numerical perturbations: the perfectly symmetric setup will start turning left or right, depending on how the approximation errors build up. Averaging the two modes would give an unphysical, straight flow similar to the parabola example above.
Similarly, we have different modes in many numerical solutions, and typically it’s important to recover them, rather than averaging them out. Hence, we’ll show how to leverage training via differentiable physics in the following chapters for more practical and complex cases.
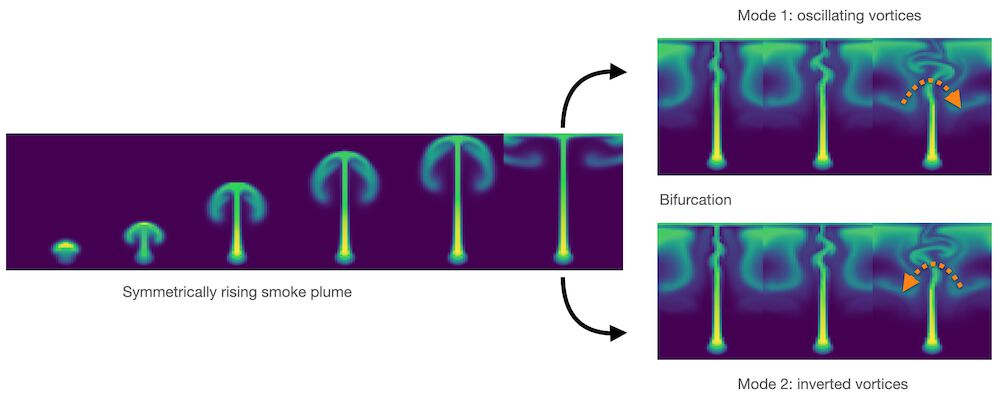
Fig. 3 A bifurcation in a buoyancy-driven fluid flow: the “smoke” shown in green color starts rising in a perfectly straight manner, but tiny numerical inaccuracies grow over time to lead to an instability with vortices alternating to one side (top-right), or in the opposite direction (bottom-right).#
Next steps#
For each of the following notebooks, there’s a “next steps” section like the one below which contains recommendations about where to start modifying the code. After all, the whole point of these notebooks is to have readily executable programs as a basis for own experiments. The data set and NN sizes of the examples are often quite small to reduce the runtime of the notebooks, but they’re nonetheless good starting points for potentially complex and large projects.
For the simple DP example above:
This notebook is intentionally using a very simple setup. You can change the training setup or network architectures to improve the solutions. E.g., provide more samples around zero to improve the solution near the origin.
Or try extending the setup to a 2D case, i.e. a paraboloid. Given the function \(\mathcal P:(y_1,y_2)\to y_1^2+y_2^2\), find an inverse function \(f\) such that \(\mathcal P(f(x)) = x\) for all \(x\) in \([0,1]\).
If you want to experiment without installing anything, you can also [run this notebook in colab].